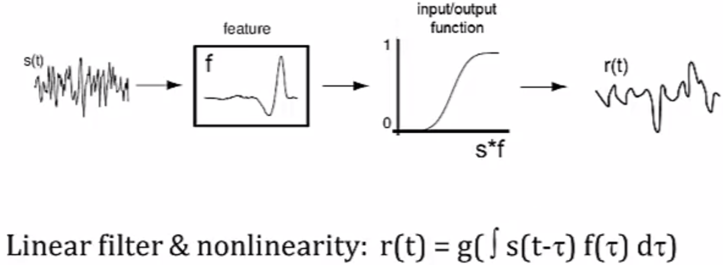
2.2 Neural Encoding: Simple Models
Constructing response models
- Our goal here is to learn methods for finding out what components of a stimulus a neural system responds to and the response function that links stimulus to a response
Basic coding model: temporal filtering
- We expect that the response depends not just on the stimulus at some particular time in the past but on some combination of recent inputs
- We can accomplish this with linear filters
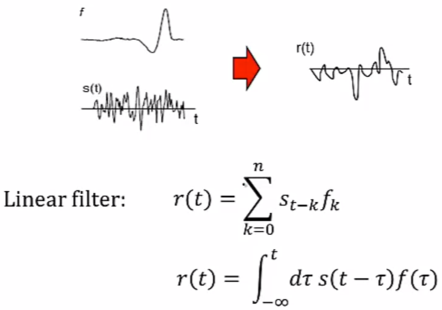
- An intuitive way to think of temporal filtering is to imagine that the system is scanning the stimulus wave-form by sliding a window of a certain width/duration along it
- The more the stimulus in the window resembles the filter, the more strongly the system will respond
- Thus, the system is “looking for” pieces of the stimulus that resemble the filter
Spatial filtering and receptive fields: difference of Gaussians
- The Gaussians here are not probability distributions; they just indicate the mathematical form of the filter
\[
r(x,y)=\sum^n_{x'--n,y'=-n}s_{x-x',y-y'}f_{x-x',y-y'}
\]


Next most basic coding model
- The problem with our current model which only consists of a filtered signal is that it could output extremely negative or positive firing rates which are impossible in real life
- To solve this we use an input/output function which transforms the linearly filtered signal to a signal whose value lies between 0 and 1